Draw a bunch of points randomly on a page. Most likely, what you drew is a set of points that are not quite statistically independent, yet not very ordered: this is an example of correlated disorder. Correlated disordered structures have been of great interest in recent years to a large number of communities, from random geometry to optics going through statistical physics.

A long-standing problem is that of being able to produce point patterns with specified features in their correlations. From the mathematical perspective, it is still not clear what precise conditions ensure that correlations are actually realizable by a point pattern. From a computer science perspective generating such point patterns is crucial to control the cost-error trade-off of Monte Carlo samplers, for instance in rendering. From a physical perspective, generating patterns with specified correlations is an important step in the design of disordered metamaterials, that display desirable transport properties thanks to their correlations yet are isotropic and resilient against perturbations thanks to their inherent disorder.

In recent years, I have produced an efficient algorithm to produce such patterns at lightning speed, and I have applied the algorithm to produce new disordered materials that display isotropic bandgaps.

Fast generation of Spectrally-shaped disorder

Producing point patterns with specified features in their correlations can be a daunting task. From a physical perspective, one often relies on simple heuristics on the effect of interactions between particles to self-assemble specific patterns. Yet, this approach is very tedious: the link between a microscopic interaction and finite-density patterns is generally non-trivial as it depends on high-order correlations in the system.

Inspired by the collective-variable approach pioneered by Sal Torquato and co-workers, we thus proposed to impose correlation features in point patterns by an optimization protocol, where a loss is defined via the difference between the observed Fourier-space representation of correlations (the Structure Factor S) and a target value S₀ defined over a finite collection of Fourier variables. Such algorithms were already proposed, but suffered very bad scalings of the number of required operations with size, O(N³) with the number N of points, in past works. As a result, this route was limited to N a few thousand at most, and was computationally intensive even then.

The trick in our work was to notice that for our choice of loss, both the loss and its gradient with respect to point positions can be written as Non-Uniform Fast Fourier Transforms (nuFFTs), taking down the computational complexity to O(N log N) . This constitutes the core of our Fast Reciprocal-Space Correlator, or FReSCo for short.

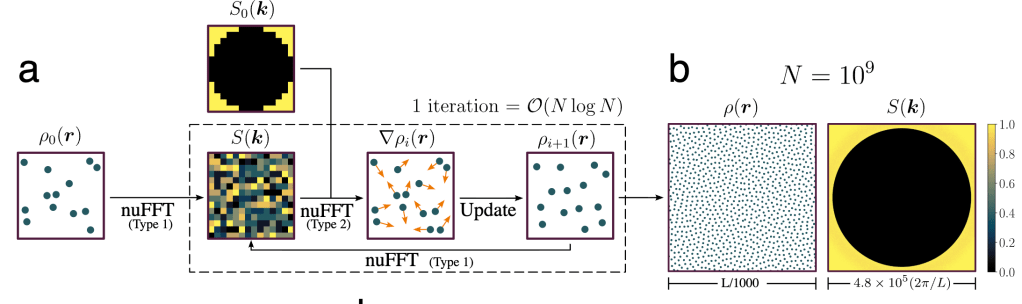
We demonstrated this very favorable scaling in a simple case that attracted a lot of attention in recent years, so-called stealthy hyperuniform systems where S₀ = 0 near the origin of Fourier space, and demonstrated that we could produce point patterns as large as a billion points on a single CPU in a matter of a day, as opposed to months on a CPU to produce similar structures with 10000 points in past work. We then demonstrated that this strategy achieved similarly good performance to impose more intricate targets, isotropic or anisotropic, as long as they were realizable.

We also demonstrated a number of extensions of the algorithm, for instance to produce specified correlations in random fields while retaining the same scaling, or to constrain systems with free boundary conditions rather than periodic ones. Furthemore, we showed that co-optimization with additional constraints like repulsion retained the same scaling.

This algorithm opens up wide avenues for future work in various directions. From a practical perspective, one may now generate much larger point patterns to test mathematical hypotheses on asymptotically large ones, or to print them as full-fledged metamaterials with long-range correlations. From a fundamental perspective, this algorithm may also be combined with methods designed to study loss landscapes (see, e.g., my own work) to characterize the realizability of certain correlations in the presence of other geometric constraints, for instance in real systems of hard spheres.

This work has been published in PRE, where it was an Editor’s Suggestion and Featured in Physics. Furthermore, a video illustrating this work (shown below) received the video Prize of the 2024 Gallery of Soft Matter of the APSDSOFT (Press Coverage, Editorial).

Correlated disorder as metamaterials: introducing gyromorphs

Having gained the ability to impose arbitrary correlations in point patterns, we sought to apply this method to propose new materials design for specific functions. In recent years, a lot of attention has been devoted to the design and discovery of isotropic bandgap materials, structures that stop light from propagating through them around a particular frequency and for all incoming wave orientations.

Notable past candidates to produce this function have been stealthy hyperuniform structures, for which the structure factor S is close to 0 near the origin of Fourier space, high-order quasicrystals in which the anisotropy becomes less noticeable, and Vogel spirals, deterministic structures observed in sunflower heads. We argue that the commonalities between these structures are that they display a low-high-low radial profile of their structure factor near the wavenumber of interest, and core exclusion in real space.

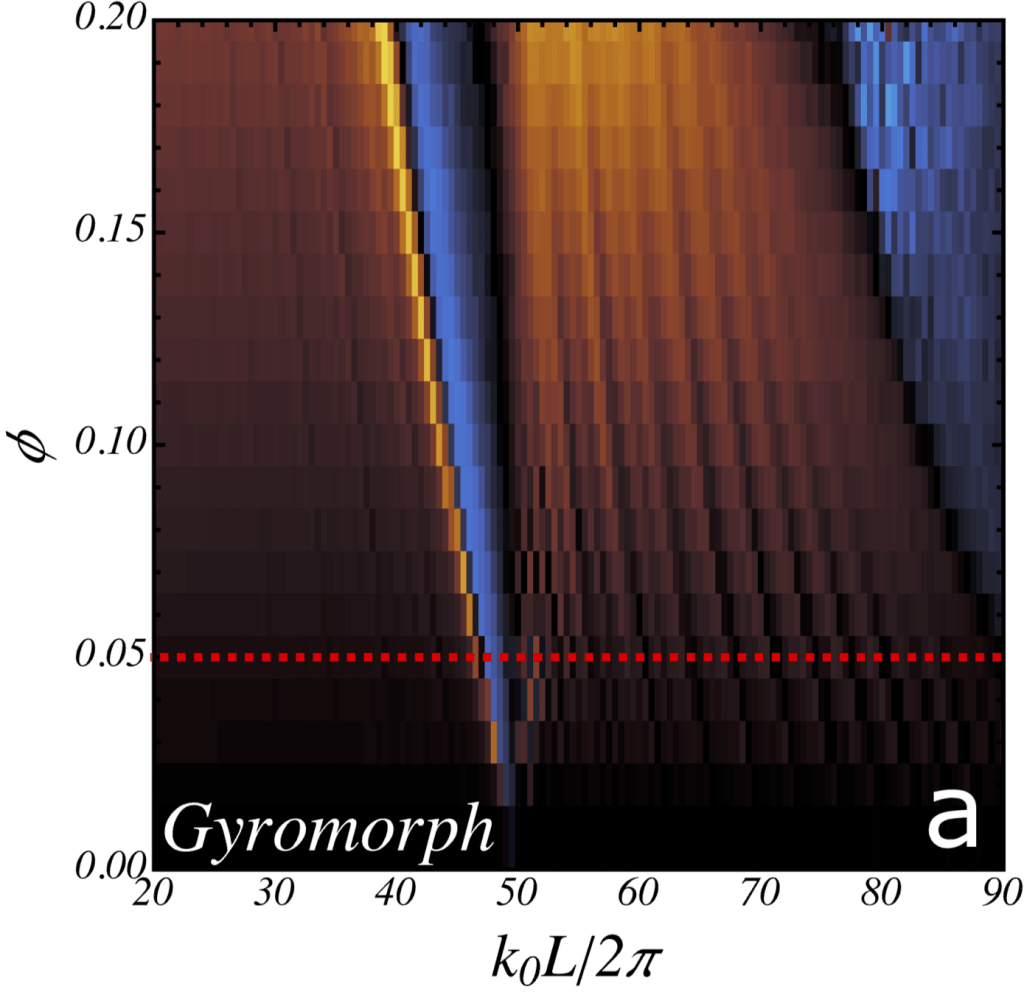
We thus propose a new class of structures, that we name gyromorphs, that are optimized to display G maximally high peaks on a ring while displaying no overlapping points. These structures are realizable by FReSCo.

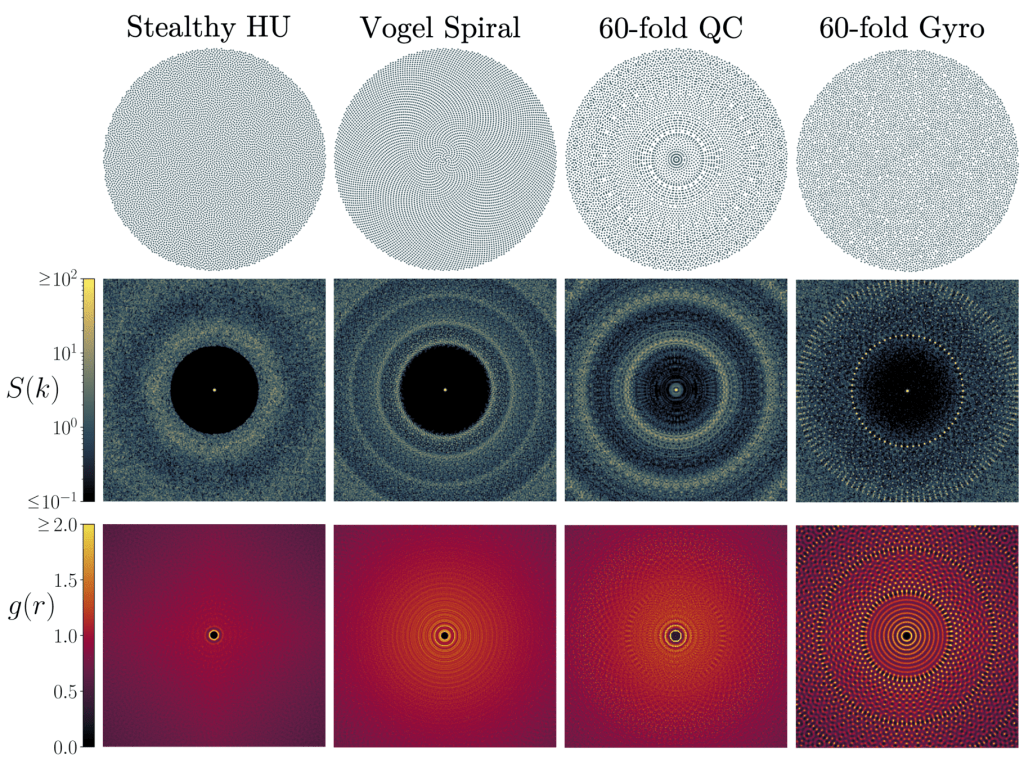
Gyromorphs are surprising structures that dislay isotropic order at short range and only break isotropy at a range that scales linearly with the number of peaks on the ring. They have peaks that scale like Bragg peaks with the number of points, yet are not quasiperiodic or even hyperuniform. In that sense, they are reconciling liquid-like isotropic correlations with quasicrystal-like high peaks.

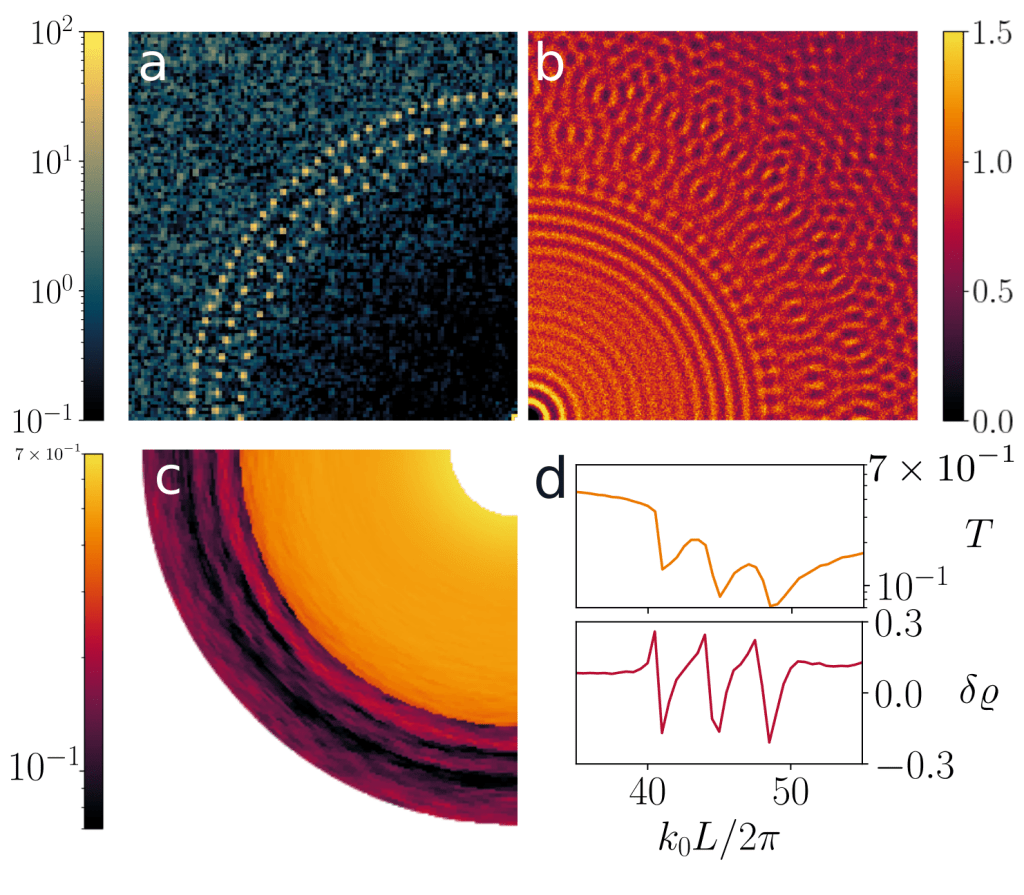
To assess the optical properties of aperiodic structures with N > 10000 points, we resort to the coupled dipole methods, which reduces the problem to one linear system to solve. Other advantages of this method are that it allows us to work with a finite chunk of material in free space rather than the less realistic case of periodicized patterns, and that it lets us compute the full field anywhere in space for any choice of source at a much lower cost than finite-difference methods. We thus shine Gaussian beams with various fewquencies and orientations at the system to assess its transmission properties.

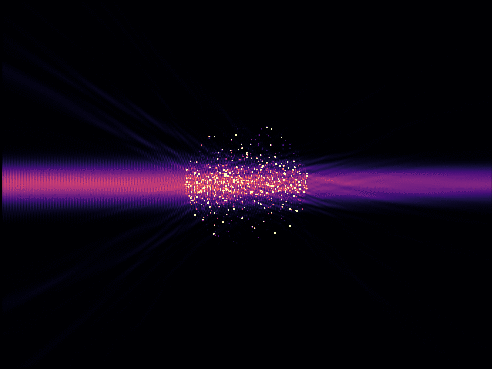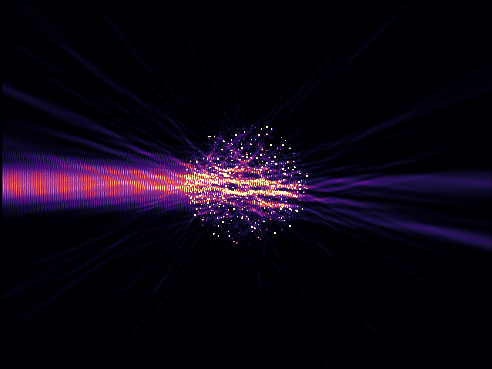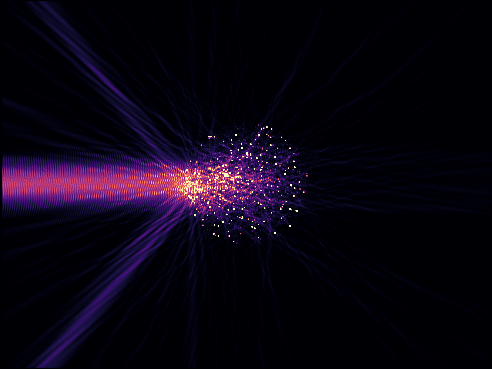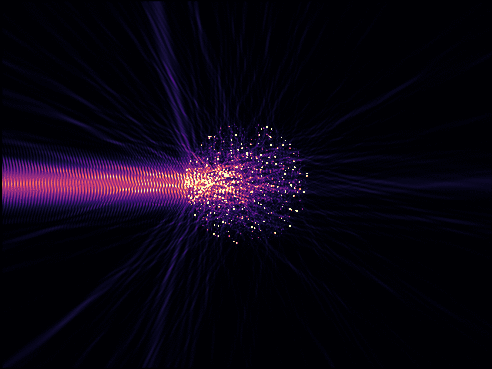
Recording the transmission through the system, we report that gyromorphs display isotropic transmission gaps over a wide range of optical parameters, and that the transmission gap is associated to a depletion of the density of states (DOS) comparable to that observed in other candidate systems, in both vector and scalar waves.

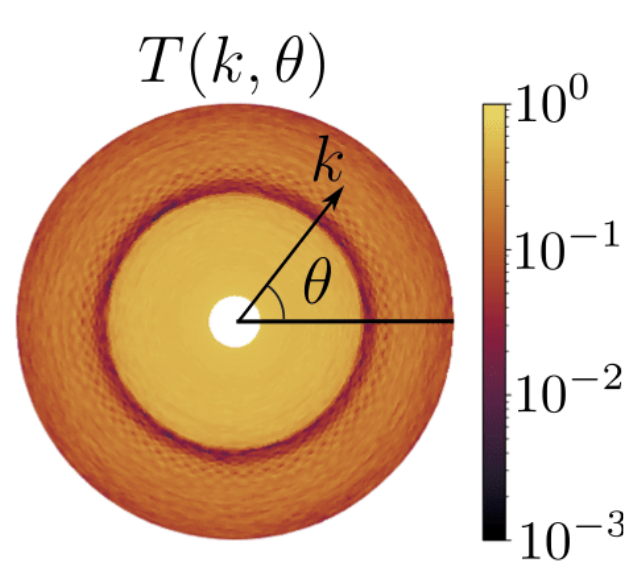
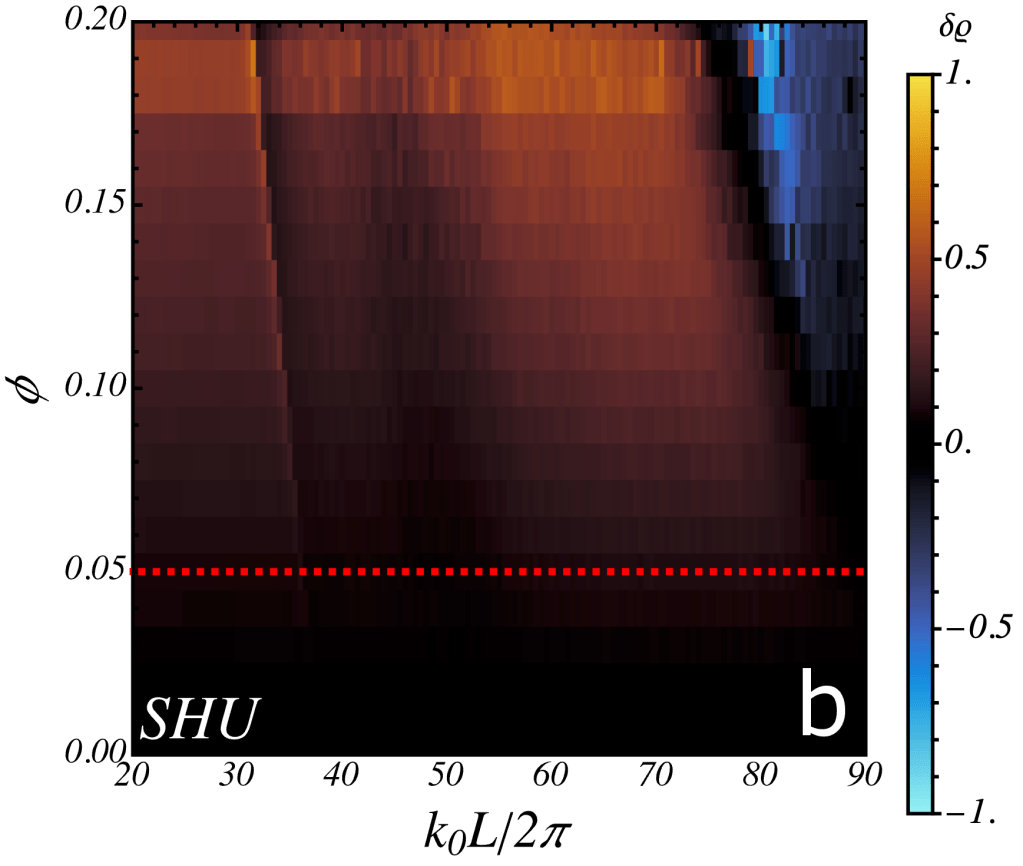
Emboldened by this confirmation of our heuristic to form bandgaps, we highlight that similar ideas can be exploited in the future to produce more intricate optical function. We showed, for instance, that the definition of gyromorphs as well as their properties hold in 3d or, along a less obvious direction, that one may create polygyromorphs, structures with several concentric rings of high peaks and very little correlations otherwise. These structures are clearly distinct from any previously known one, and display suppressed optical transmissions at 3 features, highlighting the potency of FReSCo as a materials design tool.

Much work is yet to fully exploit the possibilities of point patterns with user-specified Fourier-space correlations in the realm of designer materials. We aim to collaborate with experimental opticists to fully integrate this method within the toolbox of materials scientists.

This work has been published as an Editor’s Suggestion in Physical Review Letters.

It has attracted some attention in the specialized press, and has in particular been featured in Optica’s Optics and Photonics News, the Optics equivalent of Physics for the APS.